문제 링크
https://school.programmers.co.kr/learn/courses/30/lessons/92344
프로그래머스
SW개발자를 위한 평가, 교육, 채용까지 Total Solution을 제공하는 개발자 성장을 위한 베이스캠프
programmers.co.kr
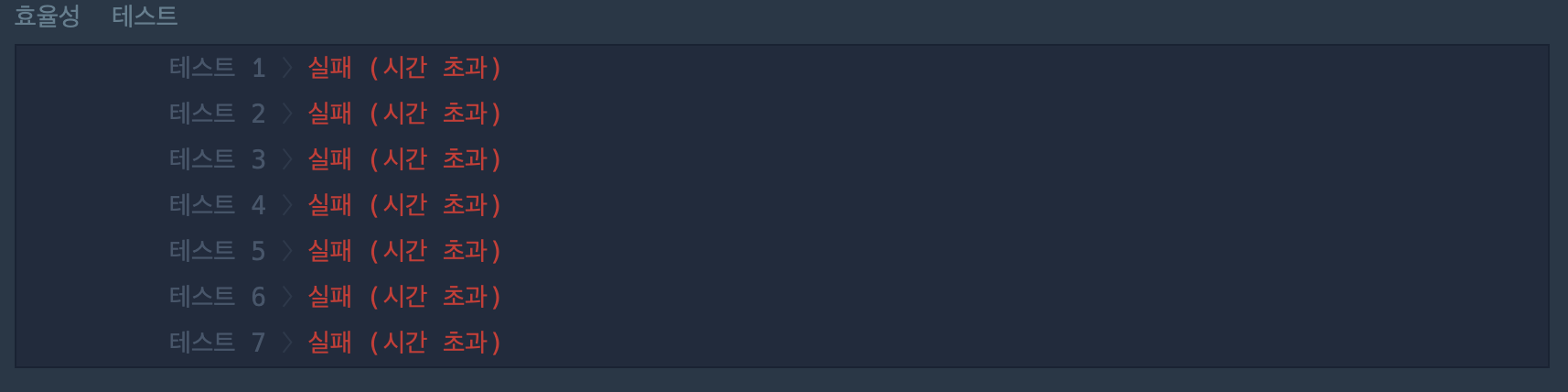
효율성 테스트 실패 코드
효율성을 고려하지 않고 Brute Force 방식으로 코드를 작성한다면, 굉장히 쉬운 문제다.
class Solution {
public int solution(int[][] board, int[][] skill) {
for (int[] s : skill) {
if (s[0] == 1) { // 공격
for (int i=s[1]; i<=s[3]; i++) {
for (int j=s[2]; j<=s[4]; j++) {
board[i][j] -= s[5];
}
}
} else { // 회복
for (int i=s[1]; i<=s[3]; i++) {
for (int j=s[2]; j<=s[4]; j++) {
board[i][j] += s[5];
}
}
}
}
int answer = 0;
for (int[] b : board) {
for (int x : b) {
if (x > 0) {
answer++;
}
}
}
return answer;
}
}위와 같이 반복문을 돌면서, board 배열의 값들을 수정한 후, 다시 board 전체 배열의 값들을 확인하면서 파괴되지 않는 건물의 개수를 세어주면 된다. 하지만, 이 코드의 시간 복잡도는 O(N * M * K)으로 이렇게 작성할 경우, 효율성 테스트에서 모두 시간 초과가 발생하는 결과가 나오게 된다.
어떻게 시간 복잡도를 줄일 수 있을까?
누적 합 이용
이 문제는 2차원 배열에서 구간의 변화를 어떻게 효율적으로 처리할 지가 관건인 문제로, 누적합을 이용하면 효율적으로 처리할 수 있다.
1차원 배열에서의 누적 합
[1,2,4,8,9]의 num 배열이 있고, 0번째부터 2번째 원소까지 2만큼 빼야 하는 상황이라고 가정해보자. 반복문을 사용해, O(M)의 시간 복잡도로 모든 원소를 순회하며 2를 빼주어도 좋지만, 이를 O(1)로 만들기 위해서는 우선 [-2,0,0,2,0,0]를 저장한 새로운 diff 배열을 생성하는 것이다. 여기서, 2번째 인덱스의 값에 2를 저장하는 것이 아니라 3번째 인덱스의 값에 2를 저장하는 것을 유의하자. 이유는 아래 사진과 같다.
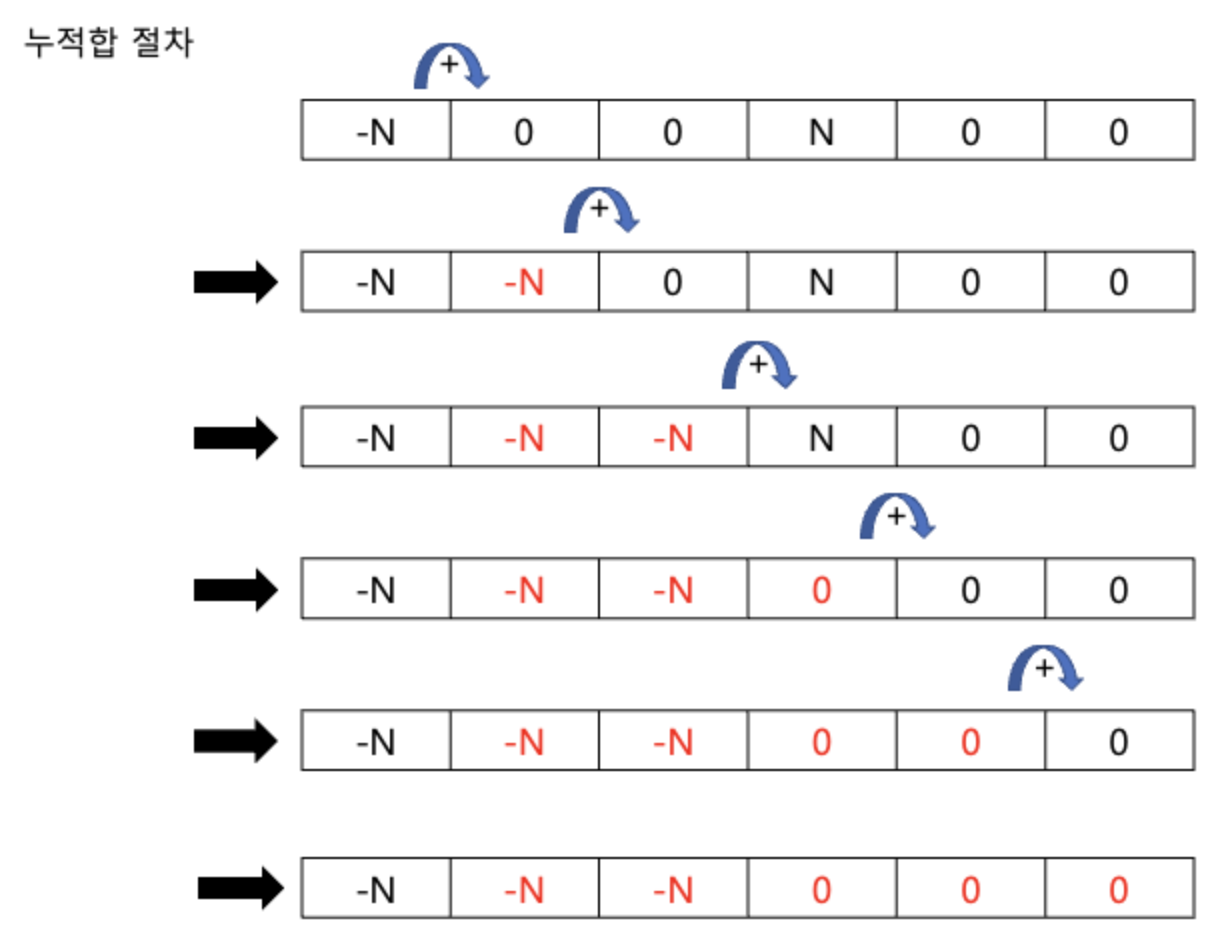
이 diff 배열을 누적합하여([-2,-2,-2,0,0,0]) 본래의 num 배열과 더해주면 [-1,0,2,8,9]을 얻을 수 있게 된다.
2차원 배열에서의 누적합
이 아이디어를 2차원 배열로 확장해보자. 5x5배열에서 (0,0)~(2,2)까지 N만큼 감소시키는 경우를 생각해보자.
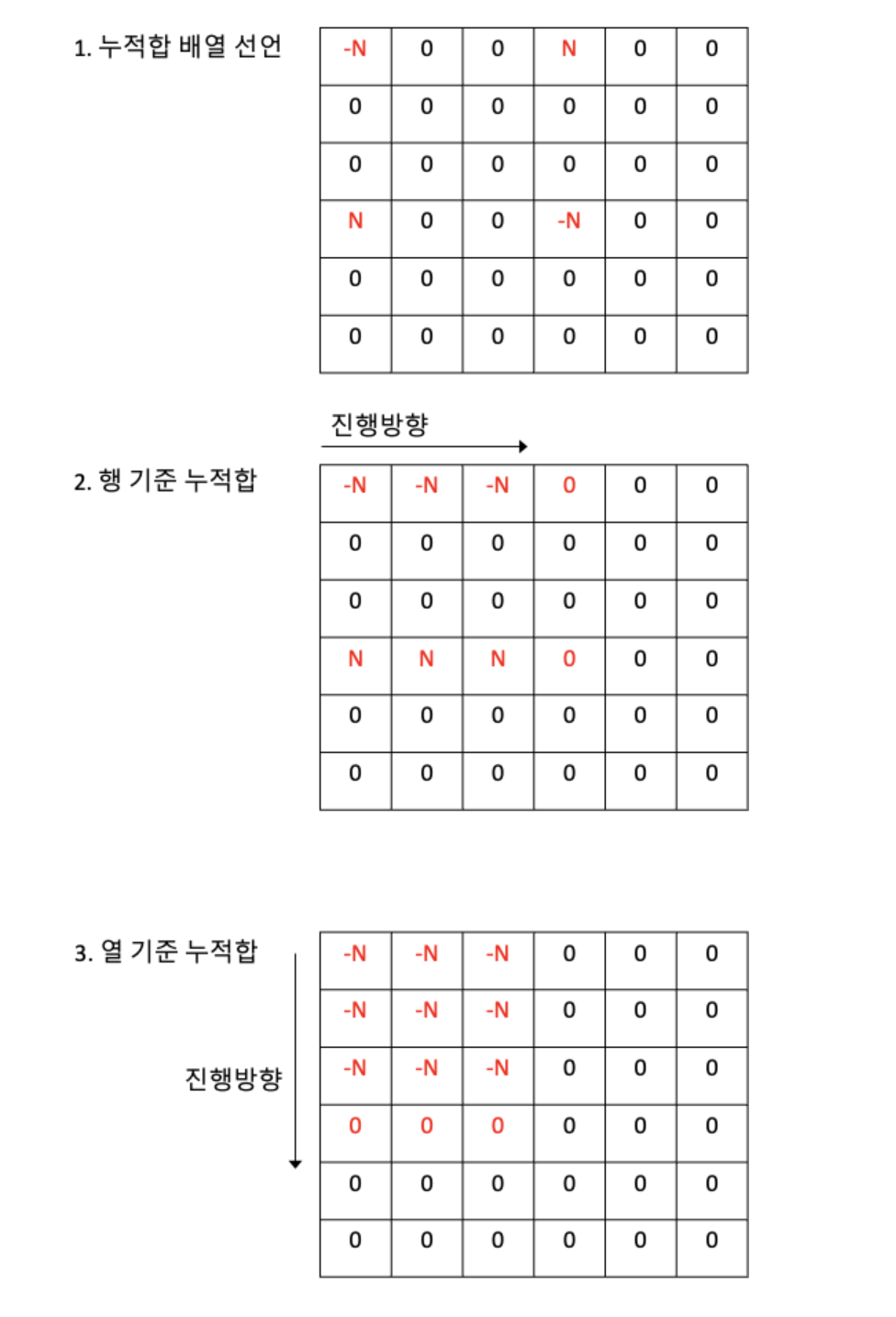
즉, 2차원 배열에서 (x1,y1)부터 (x2,y2)까지 n만큼의 변화는 (x1,y1)에 +n, (x1,y2+1)에 -n, (x2+1,y1)에 -n, (x2+1,y2+1)에 +n을 한 것과 같다.
해당 배열을 누적합 배열로 바꾸는데 걸리는 시간복잡도는 O(N * M), 그리고 K개의 skill을 모두 처리할 수 있는 배열을 만드는데 O(K)가 걸리게 되므로 최종적인 시간 복잡도는 O(K + N * M)이 된다.
최종 코드
class Solution {
public int solution(int[][] board, int[][] skill) {
int n = board.length;
int m = board[0].length;
int[][] diff = new int[n+1][m+1];
for (int[] s : skill) {
int type = s[0] == 1 ? -1 : 1;
int r1 = s[1], c1 = s[2], r2 = s[3], c2 = s[4];
int degree = s[5] * type;
diff[r1][c1] += degree;
diff[r1][c2+1] -= degree;
diff[r2+1][c1] -= degree;
diff[r2+1][c2+1] += degree;
}
// 행 기준 누적 합
for (int i = 0; i < n; i++) {
for (int j = 1; j < m; j++) {
diff[i][j] += diff[i][j - 1];
}
}
// 열 기준 누적 합
for (int i = 1; i < n; i++) {
for (int j = 0; j < m; j++) {
diff[i][j] += diff[i - 1][j];
}
}
int answer = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
board[i][j] += diff[i][j];
if (board[i][j] > 0) {
answer++;
}
}
}
return answer;
}
}
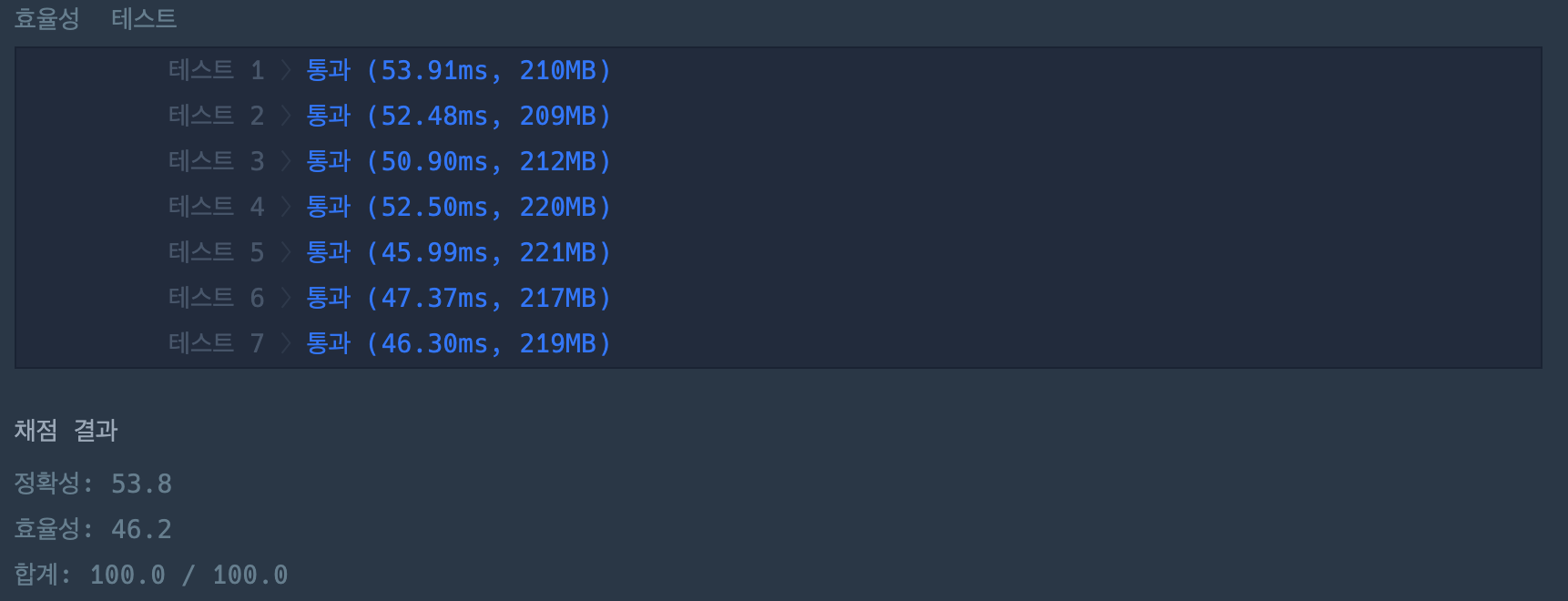
이렇게 누적합을 이용하여 코드를 구현하면 효율성 테스트를 통과할 수 있다.
'자료구조&알고리즘' 카테고리의 다른 글
| B+Tree (0) | 2025.10.01 |
|---|---|
| [BOJ] 나머지 합 (Java) - 골드 3 (0) | 2025.03.25 |
| [Programmers] 표 편집 (Java) - 2021 카카오 채용연계형 인턴십 (0) | 2025.03.17 |
| [BOJ] 행성 터널 (Java) - 플레티넘 5 (0) | 2025.03.17 |
